
Give the DFA accepting the language over the alphabet 0,1 that have the set of. 50 and one for Water at(Clicking on each layer gets an article on that subject)all strings that either begins or end(or both) with 01. Let there be two buttons, one for Coke at. Modify the soda machine so that it actually does something (i.e., some soda comes out) by converting our finite state acceptor to a finite state transducer. Recall the finite state machine that we constructed in class to accept 1.00 in change or bills.
Finite-state machines are of two types— deterministic finite-state machines and non-deterministic finite-state machines. An FSM is defined by a list of its states, its initial state, and the inputs that trigger each transition. The FSM can change from one state to another in response to some inputs the change from one state to another is called a transition.

In the unlocked state, putting additional coins in has no effect that is, giving additional coin inputs does not change the state. Putting a coin in – that is, giving the machine a coin input – shifts the state from Locked to Unlocked. In the locked state, pushing on the arm has no effect no matter how many times the input push is given, it stays in the locked state. There are two possible inputs that affect its state: putting a coin in the slot ( coin) and pushing the arm ( push). After the customer passes through, the arms are locked again until another coin is inserted.Considered as a state machine, the turnstile has two possible states: Locked and Unlocked. Depositing a coin or token in a slot on the turnstile unlocks the arms, allowing a single customer to push through.
The arrow into the Locked node from the black dot indicates it is the initial state.A state is a description of the status of a system that is waiting to execute a transition. An input that doesn't cause a change of state (such as a coin input in the Unlocked state) is represented by a circular arrow returning to the original state. Each arrow is labeled with the input that triggers that transition. Edges ( arrows) show the transitions from one state to another. Each state is represented by a node ( circle).
UML state machines overcome the limitations of traditional finite-state machines while retaining their main benefits. an exit action: performed when exiting the state.The Unified Modeling Language has a notation for describing state machines. an entry action: performed when entering the state, and Identical stimuli trigger different actions depending on the current state.In some finite-state machine representations, it is also possible to associate actions with a state: When the system is in the "CD" state, the "next" stimulus results in moving to the next track.
Other state diagrams There are a large number of variants to represent an FSM such as the one in figure 3.In addition to their use in modeling reactive systems presented here, finite-state machines are significant in many different areas, including electrical engineering, linguistics, computer science, philosophy, biology, mathematics, video game programming, and logic. SDL state machines The Specification and Description Language is a standard from ITU that includes graphical symbols to describe actions in the transition:SDL embeds basic data types called "Abstract Data Types", an action language, and an execution semantic in order to make the finite-state machine executable. They support actions that depend on both the state of the system and the triggering event, as in Mealy machines, as well as entry and exit actions, which are associated with states rather than transitions, as in Moore machines. UML state machines have the characteristics of both Mealy machines and Moore machines.
The example in figure 4 shows an acceptor that accepts the string "nice". The start state can also be an accepting state, in which case the acceptor accepts the empty string. As a rule, input is a sequence of symbols (characters) actions are not used. Once all input has been received, if the current state is an accepting state, the input is accepted otherwise it is rejected. Each state of an acceptor is either accepting or non accepting. 5: Representation of an acceptor this example shows one that determines whether a binary number has an even number of 0s, where S 1 is an accepting state and S 2 is a non accepting state.Acceptors (also called detectors or recognizers) produce binary output, indicating whether or not the received input is accepted.
An example of an accepting state appears in Fig. By definition, the languages accepted by acceptors are the regular languages.The problem of determining the language accepted by a given acceptor is an instance of the algebraic path problem—itself a generalization of the shortest path problem to graphs with edges weighted by the elements of an (arbitrary) semiring. : 18, 71An acceptor could also be described as defining a language that would contain every string accepted by the acceptor but none of the rejected ones that language is accepted by the acceptor. 5), while the set of all strings whose length is a prime number is not. For example, the set of binary strings with an even number of zeroes is a regular language (cf.
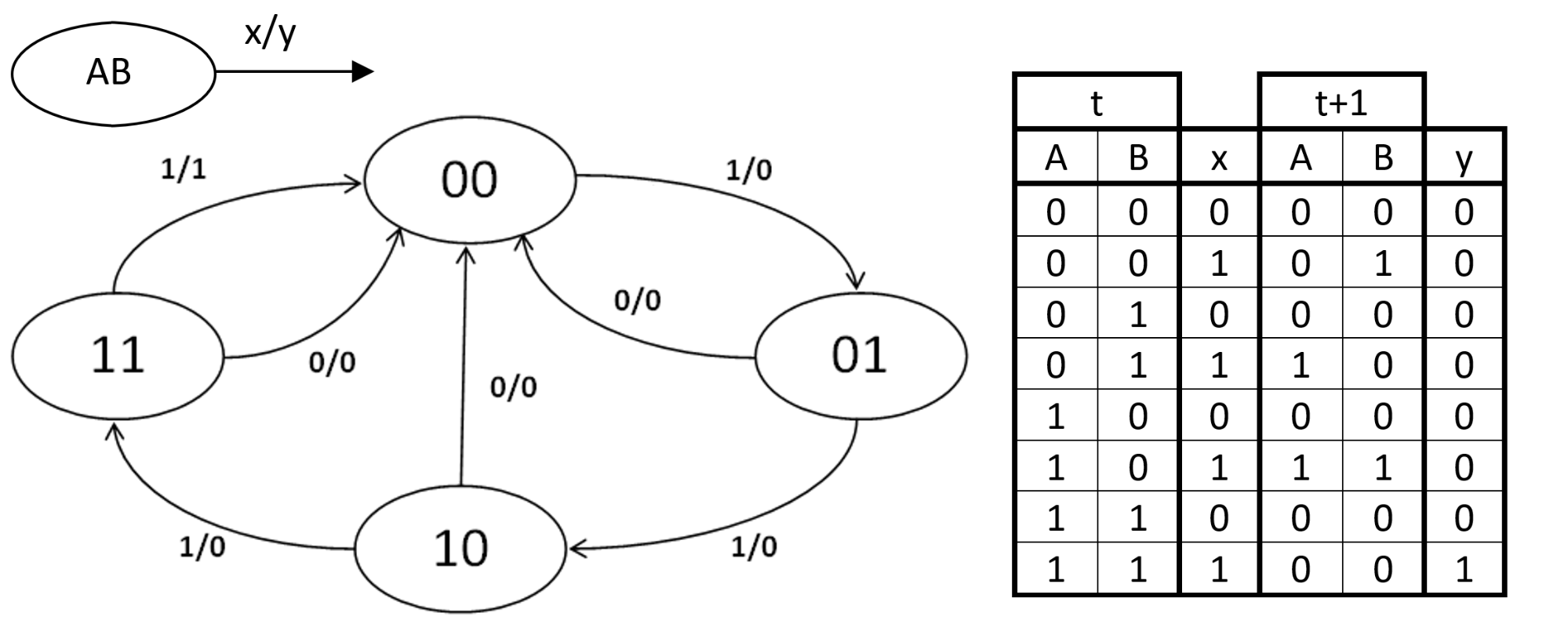
7 Transducer FSM: Mealy model exampleTransducers produce output based on a given input and/or a state using actions. Examples of strings accepted by this acceptor are ε (the empty string), 1, 11, 11., 00, 010, 1010, 10110, etc.Classifiers are a generalization of acceptors that produce n-ary output where n is strictly greater than two. This acceptor will finish in an accept state, if the binary string contains an even number of 0s (including any binary string containing no 0s). S 1 is therefore an accepting state.
Consider an elevator door. The advantage of the Moore model is a simplification of the behaviour.


 0 kommentar(er)
0 kommentar(er)
